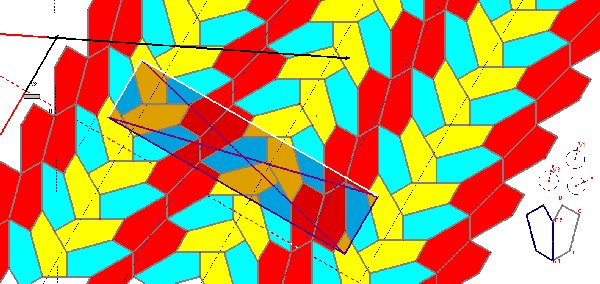
Remarque: le coté [BC] du pavé ne peut être accolé qu'à lui-même (seul de cette norme (1.93.. non multiple de 1 ou de 2) soit par symétrie axiale (paires bleu/jaune ci-dessus) , soit par symétrie centrale de centre le milieu de [BC] (paires rouges ci-dessus) mais de deux manières (deux pavés droits ou deux pavés gauches). Ces milieux sont tous centres de symétrie du pavage comme le sont aussi les milieux des cotés de longueur 1 situés sur les droites "axes" des paires rouges. Avec des pavés "physiques" découpés dans du polystyrène de 2mm, les deux cotés (2cm et 1.93cm, ou un peu plus suivant l'échelle) ne sont guère différentiables et ce n'est qu'après quelques juxtapositions que l'on se rend compte d'un petit problème.
On peut donc être tenté par l'assemblage de deux blocs par 2 côtés non compatibles:
Voir l'image avec l'erreur d'assemblage par rotation
